Rational Zero Theorem

Use the Rational Zero Theorem to Find Rational Zeros

by

Roots of a Polynomial

A root or zero of a function is a number that, when plugged in for the variable, makes the function equal to zero. Thus, the roots of a polynomial P(x) are values of x such that P(x) = 0.

Rational Zero Theorem
Rational Zero Theorem

The Rational Zeros Theorem

The Rational Zeros Theorem states:

IfP(x)is a polynomial with integer coefficients and ifis a zero of P(x)(P() = 0), thenpis a factor of the constant term ofP(x)andqis a factor of the leading coefficient of P(x).

We can use the Rational Zeros Theorem to find all the rational zeros of a polynomial. Here are the steps:

  1. Arrange the polynomial in descending order
  2. Write down all the factors of the constant term. These are all the possible values of p.
  3. Write down all the factors of the leading coefficient. These are all the possible values of q.
  4. Write down all the possible values of . Remember that since factors can be negative,  and –  must both be included. Simplify each value and cross out any duplicates.
  5. Use synthetic division to determine the values of  for which P() = 0. These are all the rational roots of P(x).

Example: Find all the rational zeros of P(x) = x3 -9x + 9 + 2x4 -19x2.

  1. P(x) = 2x4 + x3 -19x2 – 9x + 9
  2. Factors of constant term: ±1, ±3, ±9.
  3. Factors of leading coefficient: ±1, ±2.
  4. Possible values of 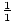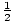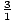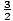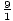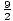: ±, ±, ±, ±, ±, ±. These can be simplified to: ±1, ±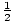, ±3, ±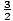, ±9, ±.
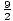  5. Use synthetic division:

Figure %: Synthetic Division

Thus, the rational roots of P(x) are x = – 3, -1, 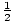, and 3.

We can often use the rational zeros theorem to factor a polynomial. Using synthetic division, we can find one real root a and we can find the quotient when P(x) is divided by x – a. Next, we can use synthetic division to find one factor of the quotient. We can continue this process until the polynomial has been completely factored.


Example (as above): Factor P(x) = 2x4 + x3 -19x2 – 9x + 9.

As seen from the second synthetic division above, 2x4 + x3 -19x2 -9x + 9÷x + 1 = 2x3 – x2 – 18x + 9. Thus, P(x) = (x + 1)(2x3 – x2 – 18x + 9). The second term can be divided synthetically by x + 3 to yield 2x2 – 7x + 3. Thus, P(x) = (x + 1)(x + 3)(2x2 – 7x + 3). The trinomial can then be factored into (x – 3)(2x – 1). Thus, P(x) = (x + 1)(x + 3)(x – 3)(2x – 1). We can see that this solution is correct because the four rational roots found above are zeros of our result.

Leave a Comment