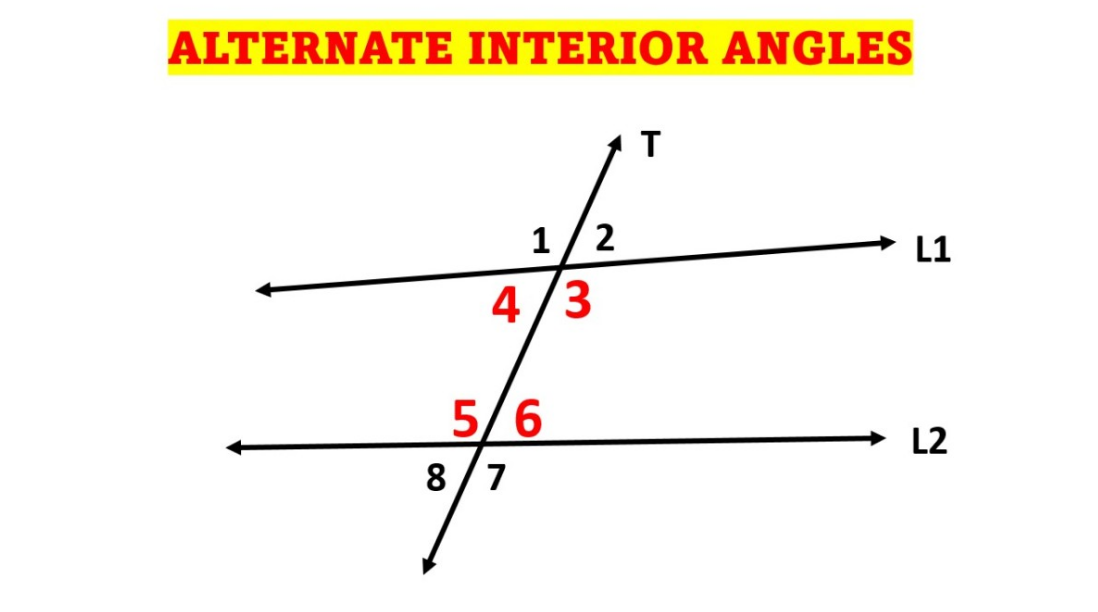
Alternate interior angles are the angles made on the opposite sides of the transversal. In other words, when two parallel lines are crossed by a transversal, eight angles are formed. Among these, the angles that lie on the inner side of the parallel lines but on the different sides of the transversal are known as the alternate interior angles.
Table of Contents
What Are Alternate Interior Angles?
When two parallel lines are intersected by a transversal, the pair of angles formed on the inner side of the parallel lines, but on the opposite sides of the transversal are called alternate interior angles. These angles are always equal. This can also be explained in another way. The alternate interior angles can determine whether the given lines are parallel or not. If these angles are equal, then the given lines which are intersected by a transversal are said to be parallel.
Examine the following figure to see the alternate interior angles. Here AB and CD are two parallel lines intersected by a transversal.
By the alternate interior angles theorem, the sets of alternate interior angles in the above figure are:
- ∠4 and ∠6
- ∠3 and ∠5
Let us briefly explain what are alternate exterior angles and how they are different from alternate interior angles.
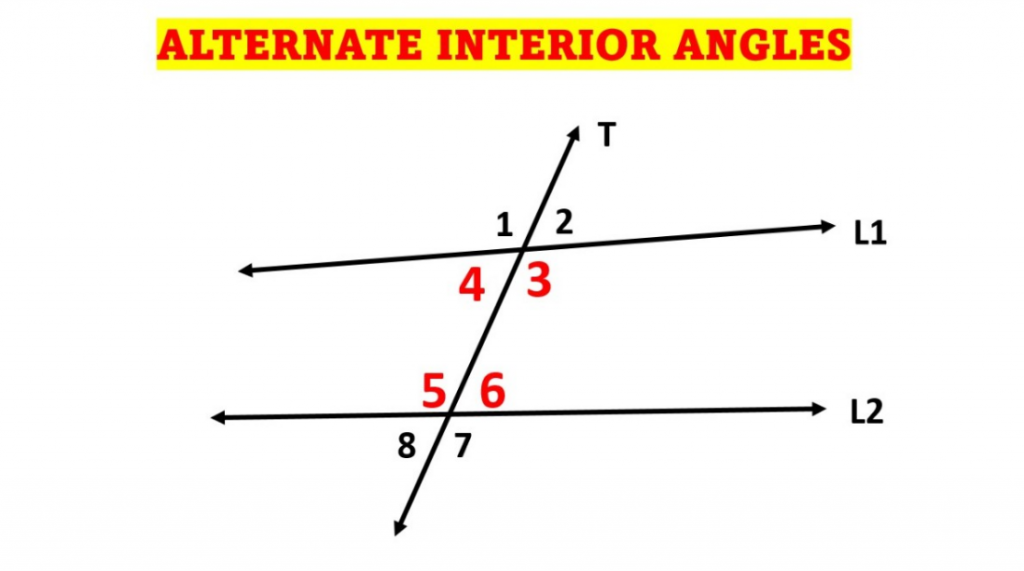
Alternate Exterior Angles
Alternate exterior angles are those angles that have several vertices, lie on the alternate sides of the transversal, and are exterior to the lines. When a transversal crosses two parallel lines, the alternate exterior angles formed are always equal. In the same figure, ∠1 & ∠7 and ∠2 & ∠8 are the sets of alternate exterior angles.
The converse of the Alternate Interior Angles Theorem
According to the converse of the alternate interior angles theorem, if a transversal crosses two lines such that the alternate interior angles are equal, then the two lines are said to be parallel.
Let us explain this with the help of the following figure which shows: ∠1 = ∠5 (corresponding angles), ∠3 = ∠5 (vertically opposite angles). Thus, ∠1 = ∠3. Similarly, we can prove that ∠2 = ∠4. This proves that since the alternate interior angles in the two presented lines are equal, these lines are parallel to each other.
How to Find the Alternate Interior Angles?
According to the alternate interior angles theorem, the alternate interior angles of two parallel lines are similar. We accept this fact to find alternate interior angles. Let us understand this with an instance.
Example: A map in which the road called Sixth Avenue runs perpendicular to the1st Street and the 2nd Street, which are parallel. Another road called Maple Avenue makes an angle of 40° with the 2nd Street. Can you get the measure of angle x?
Solution:
Following the alternate interior angles theorem, if the two streets are parallel, and Maple Avenue is supposed to be the transversal, then x and 40° are the alternate interior angles. Hence, both the angles are equal. Therefore, x = 40°.
FAQs
In geometry, to define alternate interior angles we require to check the following listed characteristics:
The alternate interior angles are equal in size.
They lie on the alternate views of the transversal.
They rest in between the interior of the two lines.
In different words, the angles that lie on the inner side of the parallel lines but on the opposite sides of the transversal.
According to the alternate interior angles theorem, if two parallel lines are intersected by a transversal, then the alternate interior angles are equal in measure. Using this theorem, we can see the measure of alternate interior angle if we know the measure of the corresponding alternate interior angle.
According to the converse of the alternate interior angles theorem, if a transversal crosses two lines such that the alternate interior angles are equal, then the two lines are said to be parallel.
Alternate interior angles are those angles that have separate vertices, they lie on the alternate sides of the transversal and are in between the interior of the two lines. Whereas alternate exterior angles are those angles that have distinct vertices, they lie on the alternate sides of the transversal, but they lie on the outer side of the two lines.
Similar angles are two angles that lie on the same side of the transversal in which one is interior and the other is exterior. The alternate angles are two angles that rest on the opposite sides of the transversal.