Parabolas are graphs of quadratic functions in mathematics. A parabola is a projective curve of a circle, according to Pascal. Galileo described a path called a parabolic path that is followed by projectiles falling under uniform gravity. In most cases, physical motions of bodies follow a curvilinear path in the shape of a parabola.
Parabolas are plane curves with mirror-symmetry and usually a U-shaped shape. In this chapter, we will trace the development of the standard formula for parabolas, demonstrate the various standard forms, and explain what properties a parabola has.
Table of Contents
What is Parabola?
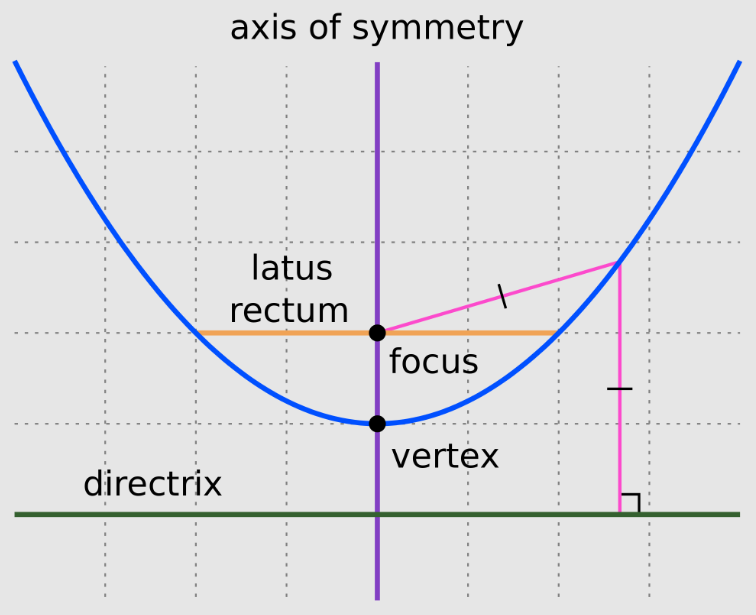
An equation of a parabola is one in which a point on the curve is equidistant from a fixed point and from a fixed-line. The fixed point is called the parabola’s focus, and the fixed line is called the directrix of the parabola.
In addition, it is important to note that the fixed point does not lie on the fixed line. Parabolas are loci of points that are equidistant from a given point (focus) and a given line (directrix). Parabolic curves are critical curves of the coordinate geometry.
Parabola Equation
As a general rule, a parabola is defined as: y = a(x-h)2 + k or x = a(y-k)2 + h, where (h,k) represents the vertex. A regular parabola is defined by the equation y2 = 4ax.
To understand some of the parts and features of a parabola, you should know the following terms.
- The focus of the parabola is the point (a, 0).
- Directrix: An imaginary line drawn parallel to the y-axis and passing through (-a, 0) is a directrix. Parabolas have parabolas that are perpendicular to their axes.
- Focal Chord: A focal chord is a chord that passes through the focus of a parabola. This chord passes through a parabola at two points.
- Focal Distance: The distance of a point (x1,y1)(x1,y1) on the parabola from the focus is the focal distance. As a result, this point is also at the same distance perpendicular to the directrix is the focal point.
- Latus Rectum: The focal chord that is perpendicular to the parabola’s axis and passes through the focus of the parabola. Latus rectum length is calculated as LL’ = 4a. (a, 2a), (a, -2a) are the endpoints of the latus rectum.
- Eccentricity: (e = 1). Basically, it is the ratio of a point’s distance from the focus to its distance from the directrix. It is equal to 1 when a parabola is considered.
Standard Equations of a Parabola
There are four standard equations for a parabola. Based on the axis and orientation of the parabola, four standard forms are available. Both the transverse and conjugate axes of these parabolas differ. The following image shows the four standard equations and parabola forms.
The following observations can be made from the standard form of equations:
- Parabola is symmetric concerning its axis. If the equation has the term with y2, then the axis of symmetry is along the x-axis, and if the equation has the term with x2, then the axis of symmetry is along the y-axis.
- When the axis of symmetry is along the x-axis, the parabola opens to the right if the coefficient of x is positive and to the left, if the coefficient of x is negative.
- The parabola opens upward if the coefficient of y is positive and downward if it is negative when the axis of symmetry is along the y-axis.
Parabola Formula
In a plane, the Parabola Formula represents the general form of a parabolic path. The following are the formulas used to find the parameters of a parabola.
- The value of a determines the direction of the parabola.
- Vertex = (h,k), where h = -b/2a and k = f(h)
- Latus Rectum = 4a
- Focus: (h, k+ (1/4a))
- Directrix: y = k – 1/4a
Graph of a Parabola
Consider the equation y = 3×2 – 6x + 5. In this parabola, a = 3, b = -6, and c = 5. Here is the graph of the given quadratic equation, which is a parabola.
a is positive, which opens up the parabola.
Vertex: (h,k)
h = -b/2a
= 6/(2 ×3) = 1
k = f(h)
= f(1) = 3(1)2 – 6 (1) + 5 = 2
Thus vertex is (1,2)
Latus Rectum = 4a = 4 × 3 =12
Focus: (h, k+ 1/4a) = (1,25/12)
Axis of symmetry is x =1
Directrix: y = k-1/4a
y = 2 – 1/12 ⇒ y – 23/12 = 0
Derivation of Parabola Equation
The parabola has coordinates (x, y) at point P. As per the definition of a parabola, the distance of this point from the focus F is equal to the length of this point P from the Directrix. For this calculation, we consider a point B on the directrix, and we use the perpendicular distance PB.
According to this definition of the eccentricity of the parabola, PF = PB (since e = PF/PB = 1)
The coordinates of the focus are F(a,0), and we can use the coordinate distance formula to find its distance from P(x, y)
PF = √(x−a)2+(y−0)2(x−a)2+(y−0)2
= √(x−a)2+y2(x−a)2+y2
X + a = 0 is the equation for the directtrix, and the perpendicular distance formula is used to find PB.
PB = x+a√12+02x+a12+02
=√(x+a)2(x+a)2
PF = PB must be used to derive the equation for parabola
√(x−a)2+y2(x−a)2+y2 = √(x+a)2(x+a)2
Squaring the equation on both sides,
(x – a)2 + y2 = (x + a)2
x2 + a2 – 2ax + y2 = x2 + a2 + 2ax
y2 – 2ax = 2ax
y2 = 4ax
We have successfully derived a standard equation for the parabola.
In the same way, we can deduce the equations for parabolas as:
- (b): y2 = – 4ax,
- (c): x2 = 4ay,
- (d): x2 = – 4ay.
The above four equations are the Standard Equations of Parabolas.
Properties of a Parabola
Here we shall aim at understanding some of the essential properties and terms related to a parabola.
Tangent: A tangent is a line that touches a parabola. A tangent to the parabola y2 = 4ax at the point of contact (x1,y1)(x1,y1) has the equation yy1=2a(x+x1)yy1=2a(x+x1).
Normal: This line passes through the point of contact and the focus of a parabola and is perpendicular to it. For a parabola y2 = 4ax, the equation of the normal passing through the point (x1,y1)(x1,y1) and having a slope of m = -y1/2a, the equation of the normal is (y−y1)=−y12a(x−x1)(y−y1)=−y12a(x−x1)
Chord of Contact: A chord drawn from the point of contact of the tangents drawn from an external point to the parabola is called a chord of contact. For a point (x1,y1)(x1,y1) outside the parabola, the equation of the chord of contact is yy1=2x(x+x1)yy1=2x(x+x1).
Pole and Polar: At the ends of the chords, draw an outside point of the parabola, the locus of the points of intersection of the tangents. The polar drawn from this point is the pole. Hence, the pole is the point to which the polar is referred. For a pole having the coordinates (x1,y1)(x1,y1), for a parabola y2 =4ax, the equation of the polar is yy1=2x(x+x1)yy1=2x(x+x1).
Parametric Coordinates: The parametric coordinates of a parabola equation are (at2, 2at). These coordinates represent all the points on the parabola.
