The axis of symmetry is a straight line that divides an object into two identical parts, thus creating one part as a mirror image of another. Folded along the axis of symmetry, the two parts become superimposed.
In terms of symmetry, the mirror line is the straight line. The horizontal, vertical, or slanting line can be used. This axis of symmetry can be seen in nature as well, such as in flowers, riverbanks, buildings, and leaves.
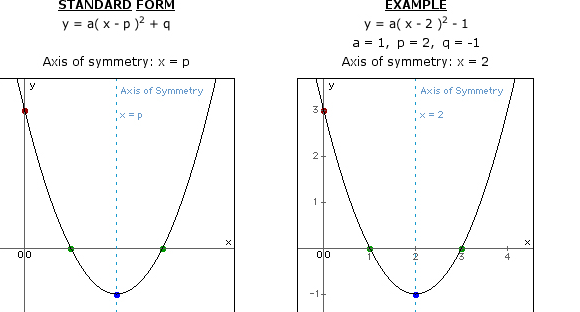
Table of Contents
What is the Axis of Symmetry?
Objects have symmetry when they are symmetrical along an axis of symmetry. Each of the sides of the symmetry axis creates an exact reflection. The two sides of an object are identical if we fold and unfold it along the axis of symmetry.
It is possible to have an axis of symmetry horizontally, vertically, or laterally. Different shapes have different lines of symmetry. A square has four lines of symmetry, a rectangle has two lines of symmetry, a circle has infinite lines of symmetry, and a parallelogram has no lines of symmetry. A regular polygon of ‘n’ sides has ‘n’ axes of symmetry.
Axis of Symmetry of a Parabola
A Parabola has one line of symmetry. The axis of symmetry is the straight line that divides a parabola into two symmetrical parts. The parabola can be in four forms. It may be horizontal or vertical, facing left or right.
The axis of symmetry determines the shape of the parabola. When the axis of symmetry is vertical, then the parabola is vertical as well. The parabola is horizontal if the axis of symmetry is horizontal.
Axis of Symmetry Equation
The vertex of a parabola is where the axis of symmetry intersects it. A parabola that opens upwards or downwards has a vertical axis of symmetry.
The equation of the axis of symmetry is the equation of the vertical line passing through the x-intercept. The axis of symmetry is horizontal if the parabola opens right or left. In mathematics, the line that passes through the y-intercept is known as the axis of the symmetry equation.
Axis of Symmetry Formula
The axis of symmetry formula helps to find the axis of symmetry of a parabola, applied to quadratic equations where the standard form of the equation and the line of symmetry are used. It is known as the axis of symmetry any line or plane creating two equally sized halves whose mirror images are the same.
In addition to the horizontal axis (x-axis), there is a vertical axis and an inclined axis to divide the objects. In geometry, a line of symmetry means the line that divides a geometric shape into two equal halves, making it appear mirror-imaged.
The equation for the axis of symmetry can be expressed in two ways:
- Standard form
- Vertex form
Standard form
The quadratic equation in standard forms, y = ax2+ b x+c
Where a, b are the coefficients of “x” and c is the constant form.
Here, the axis of symmetry formula is: x = – b/2a
Vertex form
The quadratic equation in vertex form is, y=a (x-h)2 + k
The vertex of the parabola is (h, k). In vertex form, we can say, x = h since the axis of symmetry and vertex lie on the same line: h = – b/2a
How to derive the axis of symmetry for a parabola
As the vertex of the parabola extends, the axis of symmetry passes through. Identifying the vertex allows us to calculate the location of the axis of symmetry. Axis of symmetry formula for a parabola is, x = -b/2a. Let’s find the equation for the axis of symmetry.
The quadratic equation of a parabola is, y = a x2+ b x+ c
Where (a, b) is the co-efficient of x and ‘c’ is the constant term.
‘C’ is a constant that does not affect the parabola. Therefore, let us consider y = a x2+b x.
Assume y= 0 and x= 0, which implies, a x2+b x=0
x(ax+b)=0
x = 0 and (ax+b)=0
x = -b/a
Therefore, the two values of x= (0,-b/a)
The mid-point formula is x=x1+x22x1+x22
x= 0+−ba20+−ba2
Therefore x = -b/2a
If the axis of symmetry lies on the x-axis, we take the y-intercept. y = -b/2a
Axis of Symmetry Formula Examples
Example 1: Determine the quadratic equation’s axis of symmetry using the axis of symmetry formula: y = x2 – 4x + 3.
Solution:
Given: y = x2 – 4x + 3
Using the axis of symmetry formula,
x = -b/2a
x = -(-4)/2(1)
x = 4/2
= 2
Therefore, the axis of symmetry of equation y = x2 – 4x + 3 is x = 2.
Example 2: Find the axis of symmetry of a parabola y = 4x2.
Solution:
Using the axis of symmetry formula,
x = -b/2a
x = -(0)/2(4)
= 0
Therefore, the axis of symmetry of equation y = 4x2 is x = 0.
Identification of the Axis of Symmetry
Using the formula learned in the previous section, let’s identify the axis of symmetry for the given parabola.
1) Consider equation y = x2– 3x + 4. Contrasting this with the equation of the standard form of the parabola (y = a x2+ b x+ c), we have
a = 1, b = -3 and c = 4
This is a vertical parabola. The symmetry can be determined by looking at its axis. In general, we know that the x-axis corresponds to the axis of symmetry.
We know that x = -b/2a is the equation of the axis of symmetry.
x = -(-3)/2(1) = 1.5
x = 1.5 is the axis of symmetry of the parabola y = x2– 3x + 4.
2) Let us consider another example. x = 4y2+5y+3.
Contrasting with the standard form of the quadratic equation, we get a = 4, b = 5, and c = 3. Parabolas are horizontal, and their axes of symmetry are also horizontal.
As a result, we know the equation of the axis of symmetry is on the y-axis. The equation for the symmetry axis is y = -b/2a.
y = -b/2a
y = -5/2(4)}
y = -0.625
3) Given two points (x,y) at the same distance from the vertex of the parabola, find the midpoint of these points to determine the equation of the axis of symmetry. When the two points are (3, 4) and (9, 4), then the vertex passes through the intercept, which forms the midpoint of these two points.
Thus x = (3+9)/2 = 12/2 = 6. In this instance, the axis of symmetry is defined by (6,0), the vertical line/the axis of symmetry’s required equation.
